Training A ResNet model for Channel Estimation
Now that we have a channel estimation dataset, we can train a model to receive the channel estimates at the pilot locations and predict the channel estimates for the whole channel matrix.
We use PyTorch freamework to train our models but other machine learning tools can also be used. The following diagram shows the Neural Network structure used for the channel estimation model.
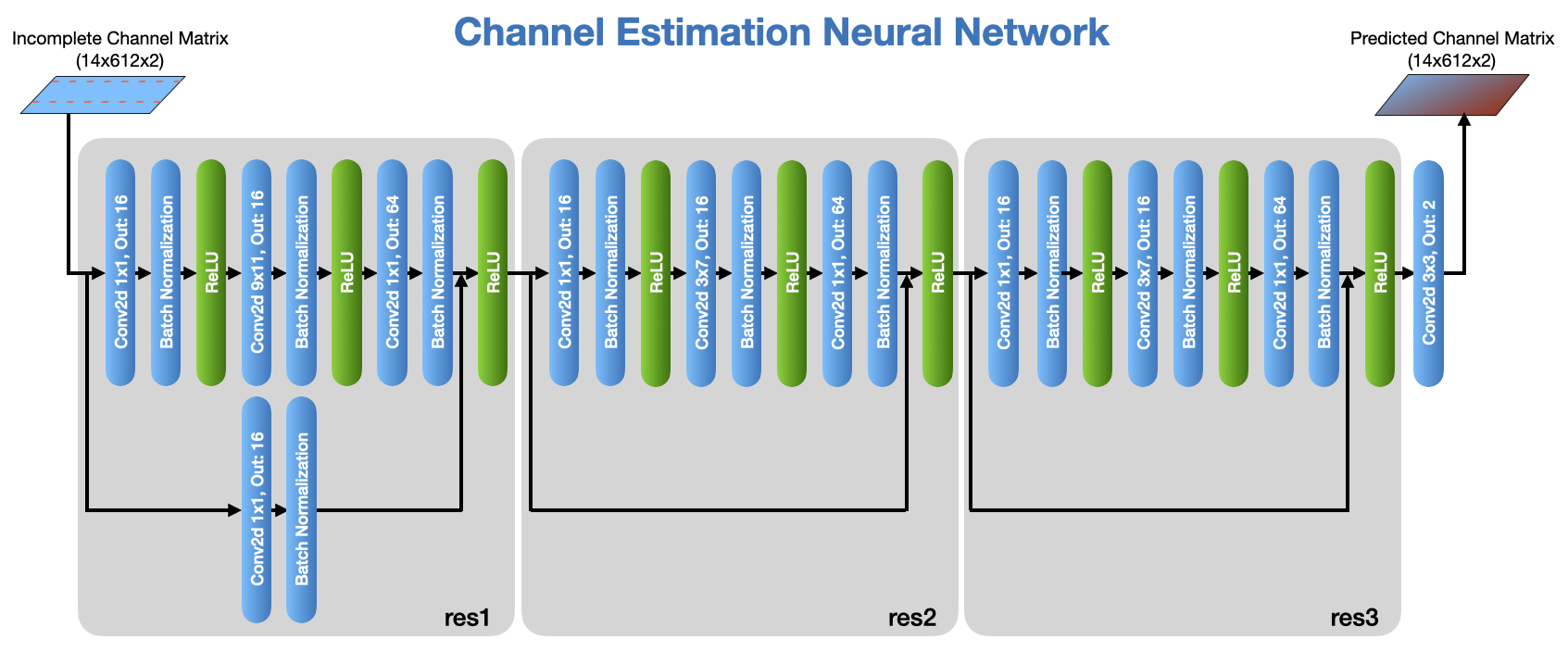
So let’s get started by importing the required modules.
[1]:
import numpy as np
import time, datetime
import torch
from torch import nn
from torch.utils.data import Dataset, DataLoader
from torch.optim.lr_scheduler import ExponentialLR
Loading dataset
We first load our dataset files generated in the previous step. Then we create three sets of datasets and dataloaders for training, validation, and test.
[2]:
# Define our dataset object
class ChEstDataset(Dataset):
def __init__(self, fileName):
samples, labels = np.load(fileName)
self.samples = np.float32(np.transpose(samples,(0,3,1,2)))
self.labels = np.float32(np.transpose(labels,(0,3,1,2)))
self.numSamples = len(self.samples)
def __len__(self):
return self.numSamples
def __getitem__(self, idx):
return self.samples[idx], self.labels[idx]
# Instantiate 3 datasets for train, validation, and test
trainDs = ChEstDataset("ChestTrain.npy")
validDs = ChEstDataset("ChestValid.npy")
testDs = ChEstDataset("ChestTest.npy")
print(f"{len(trainDs)} Training Samples")
print(f"{len(validDs)} Validation Samples")
print(f"{len(testDs)} Test Samples")
# Create the data loaders
batchSize = 64
trainDl = DataLoader(trainDs, batchSize, shuffle=True)
validDl = DataLoader(validDs, batchSize, shuffle=False)
testDl = DataLoader(testDs, batchSize, shuffle=False)
16000 Training Samples
2400 Validation Samples
2400 Test Samples
[3]:
# Checking GPU availability
device = "cuda" if torch.cuda.is_available() else "mps" if torch.backends.mps.is_available() else "cpu"
print(f"Using {device} device")
Using cuda device
Creating the model
Now we can create a model object that will be used for training. We first define the ResBlock (See the picture above)
[4]:
# Define ResNet block
class ResBlock(nn.Module):
def __init__(self, inDepth, midDepth, outDepth, kernel=(3,3), stride=(1,1)):
super().__init__()
if isinstance(stride, int): stride = (stride, stride)
if isinstance(kernel, int): kernel = (kernel, kernel)
self.conv1 = nn.Conv2d(inDepth, midDepth, 1, stride, padding='valid') # 1x1 conv.
self.bn1 = nn.BatchNorm2d(midDepth)
self.conv2 = nn.Conv2d(midDepth, midDepth, kernel, padding='same')
self.bn2 = nn.BatchNorm2d(midDepth)
self.conv3 = nn.Conv2d(midDepth, outDepth, 1, stride, padding='valid') # 1x1 conv.
self.bn3 = nn.BatchNorm2d(outDepth)
self.relu = nn.ReLU(inplace=True)
self.downSampleNet = None
if ((stride != (1,1)) or (inDepth!=outDepth)):
self.downSampleNet = nn.Sequential(nn.Conv2d(inDepth, outDepth, 1, stride), # 1x1 conv.
nn.BatchNorm2d(outDepth) )
for bn in [self.bn1, self.bn2, self.bn3]:
nn.init.ones_(bn.weight)
nn.init.zeros_(bn.bias)
for conv in [self.conv1, self.conv2, self.conv3]:
nn.init.trunc_normal_(conv.weight, std=1/np.sqrt(np.prod(list(conv.weight.shape)[1:])))
nn.init.zeros_(conv.bias)
nn.init.zeros_(self.bn3.weight) # This could improve results. It makes the block start like identity.
def forward(self, x):
out = self.conv1(x)
out = self.bn1(out)
out = self.relu(out)
out = self.conv2(out)
out = self.bn2(out)
out = self.relu(out)
out = self.conv3(out)
out = self.bn3(out)
if self.downSampleNet is None: out += x
else: out += self.downSampleNet(x)
out = self.relu(out)
return out
And now we define our Channel Estimator model (ChEstNet) using 2 instances of ResBlock defined above together with an additional convolutional layer.
[5]:
# Now the actual ChEstNet model
class ChEstNet(nn.Module):
def __init__(self):
super().__init__()
self.res1 = ResBlock(2, 16, 64, (9,11)) # Res Block 9x11 kernel
self.res2 = ResBlock(64, 16, 64, (3,7)) # Res Block 3x7 kernel
self.res3 = ResBlock(64, 16, 64, (3,7)) # Res Block 3x7 kernel
self.conv = nn.Conv2d(64, 2, 3, padding='same')
nn.init.trunc_normal_(self.conv.weight, std=1/np.sqrt(np.prod(list(self.conv.weight.shape)[1:])))
nn.init.zeros_(self.conv.bias)
def forward(self, x):
out = self.res1(x)
out = self.res2(out)
out = self.res3(out)
out = self.conv(out)
return out
# Instantiate the model and move it the target device
model = ChEstNet().to(device)
Training the model
Now we first create functions for the training and evaluation loops and use them to train the model.
Note: The following cell can take several hours to complete. A file containing the trained parameters of the model is included in this directory, so you can skip the following cells and proceed to the next step.
[6]:
# Training loop for one epoch:
def trainEpoch(dataLoader, model, lossFunction, optimizer):
modelDevice = next(model.parameters()).device
model.train() # Set the model to training mode
lossMin, lossMean, lossMax = np.inf, 0, -np.inf
for batchNo, (batchSamples, batchLabels) in enumerate(dataLoader):
# Compute prediction and loss
batchPredictions = model( batchSamples.to(modelDevice) )
loss = lossFunction(batchPredictions, batchLabels.to(modelDevice))
loss.backward() # Backpropagation
optimizer.step()
optimizer.zero_grad()
lossValue = loss.item()
lossMean += lossValue
if lossValue>lossMax: lossMax = lossValue
if lossValue<lossMin: lossMin = lossValue
lossMean /= len(dataLoader)
return lossMin, lossMean, lossMax
# Evaluation loop:
def evaluate(dataLoader, model, lossFunction):
modelDevice = next(model.parameters()).device
model.eval() # Set the model to evaluation mode
numBatches = len(dataLoader)
lossMean = 0
with torch.no_grad():
for batchNo, (batchSamples, batchLabels) in enumerate(dataLoader):
batchPredictions = model( batchSamples.to(modelDevice) )
lossMean += lossFunction(batchPredictions, batchLabels.to(modelDevice)).item()
lossMean /= numBatches
return lossMean
numEpochs = 100 # Number of epochs
learningRate = (0.0001, 0.000001) # Learning rate starts at 0.0001 and exponentially decays to 0.000001
lossFunction = nn.MSELoss() # Using MSE as Loss
if isinstance(learningRate,tuple): # learningRate is a tuple -> use exponentially decaying learning rate
from torch.optim.lr_scheduler import ExponentialLR
lr1st, lrLast = learningRate
optimizer = torch.optim.Adam(model.parameters(), lr=lr1st)
lrScheduler = ExponentialLR(optimizer, np.exp(np.log(lrLast/lr1st)/(numEpochs-1)))
else:
optimizer = torch.optim.Adam(model.parameters(), lr=learningRate) # learningRate is a number
lrScheduler = None # No LR scheduling needed
t0 = time.time()
print("Epoch Learning Rate Training Loss Validation Loss")
print("----- ------------- ------------- ---------------")
lowestLoss = None
for epoch in range(numEpochs):
print(" %-4d %-10f "%(epoch+1, lrScheduler.get_last_lr()[0]), end="")
lossMin, lossMean, lossMax = trainEpoch(trainDl, model, lossFunction, optimizer)
print("%-10f "%(lossMean), end="")
validLoss = evaluate(validDl, model, lossFunction)
if lowestLoss is None:
lowestLoss = validLoss
print("%-10f "%(validLoss))
elif validLoss<lowestLoss: # This is the best model so far -> Save it
lowestLoss, bestEpoch = validLoss, epoch+1
torch.save(model.state_dict(), 'Models/ChEstModelWeights.pth')
print("%-10f * "%(validLoss)) # The '*' indicates best so far and saving
else:
print("%-10f "%(validLoss))
if lrScheduler is not None: lrScheduler.step()
print("Training complete. (Training Time: %s)"%(str(datetime.timedelta(seconds=int(time.time()-t0)))))
Epoch Learning Rate Training Loss Validation Loss
----- ------------- ------------- ---------------
1 0.000100 0.099336 0.010627
2 0.000095 0.005880 0.004009 *
3 0.000091 0.003341 0.003787 *
4 0.000087 0.002642 0.003150 *
5 0.000083 0.002353 0.002327 *
6 0.000079 0.002188 0.003565
7 0.000076 0.002081 0.002741
8 0.000072 0.001991 0.002619
9 0.000069 0.001922 0.006631
10 0.000066 0.001875 0.001991 *
11 0.000063 0.001824 0.005979
12 0.000060 0.001783 0.002245
13 0.000057 0.001759 0.002502
14 0.000055 0.001732 0.005101
15 0.000052 0.001710 0.006416
16 0.000050 0.001689 0.007298
17 0.000048 0.001672 0.002904
18 0.000045 0.001651 0.002459
19 0.000043 0.001642 0.001740 *
20 0.000041 0.001626 0.003589
21 0.000039 0.001617 0.005713
22 0.000038 0.001604 0.001715 *
23 0.000036 0.001600 0.008538
24 0.000034 0.001587 0.002987
25 0.000033 0.001580 0.001638 *
26 0.000031 0.001572 0.001692
27 0.000030 0.001561 0.007471
28 0.000028 0.001556 0.002036
29 0.000027 0.001553 0.001821
30 0.000026 0.001550 0.009173
31 0.000025 0.001543 0.001734
32 0.000024 0.001539 0.001667
33 0.000023 0.001532 0.002818
34 0.000022 0.001528 0.001524 *
35 0.000021 0.001524 0.002134
36 0.000020 0.001523 0.003879
37 0.000019 0.001518 0.004665
38 0.000018 0.001515 0.002332
39 0.000017 0.001511 0.001507 *
40 0.000016 0.001508 0.002086
41 0.000016 0.001507 0.001654
42 0.000015 0.001502 0.004450
43 0.000014 0.001501 0.001833
44 0.000014 0.001501 0.001561
45 0.000013 0.001495 0.002375
46 0.000012 0.001497 0.001502 *
47 0.000012 0.001492 0.001637
48 0.000011 0.001494 0.001482 *
49 0.000011 0.001489 0.001800
50 0.000010 0.001487 0.001888
51 0.000010 0.001485 0.001501
52 0.000009 0.001484 0.002236
53 0.000009 0.001481 0.002009
54 0.000008 0.001482 0.001516
55 0.000008 0.001483 0.001748
56 0.000008 0.001479 0.001698
57 0.000007 0.001476 0.001729
58 0.000007 0.001482 0.001572
59 0.000007 0.001477 0.001511
60 0.000006 0.001474 0.001515
61 0.000006 0.001475 0.001533
62 0.000006 0.001471 0.001487
63 0.000006 0.001471 0.001529
64 0.000005 0.001473 0.001546
65 0.000005 0.001476 0.001488
66 0.000005 0.001472 0.001477 *
67 0.000005 0.001467 0.001483
68 0.000004 0.001470 0.001610
69 0.000004 0.001470 0.001461 *
70 0.000004 0.001467 0.001480
71 0.000004 0.001466 0.001468
72 0.000004 0.001465 0.001454 *
73 0.000004 0.001465 0.001468
74 0.000003 0.001465 0.001503
75 0.000003 0.001464 0.001458
76 0.000003 0.001463 0.001510
77 0.000003 0.001465 0.001461
78 0.000003 0.001462 0.001459
79 0.000003 0.001463 0.001452 *
80 0.000003 0.001464 0.001558
81 0.000002 0.001462 0.001476
82 0.000002 0.001463 0.001454
83 0.000002 0.001462 0.001475
84 0.000002 0.001460 0.001508
85 0.000002 0.001463 0.001491
86 0.000002 0.001462 0.001494
87 0.000002 0.001460 0.001454
88 0.000002 0.001458 0.001521
89 0.000002 0.001461 0.001483
90 0.000002 0.001462 0.001453
91 0.000002 0.001459 0.001519
92 0.000001 0.001455 0.001471
93 0.000001 0.001460 0.001474
94 0.000001 0.001461 0.001458
95 0.000001 0.001462 0.001468
96 0.000001 0.001457 0.001454
97 0.000001 0.001459 0.001464
98 0.000001 0.001459 0.001469
99 0.000001 0.001461 0.001459
100 0.000001 0.001458 0.001489
Training complete. (Training Time: 0:51:55)
Evaluating the model
[7]:
testLoss = evaluate(testDl, model, lossFunction)
print(f"Test Loss: %.6f"%(testLoss))
Test Loss: 0.001446
[ ]: