Evaluating the Trained Channel Estimator
Now that we have a trained model, we can use it in the communication pipeline and compare its performance with baselines. In this case we compare it with perfect channel estimation and NeoRadium’s Least-Square channel estimation method.
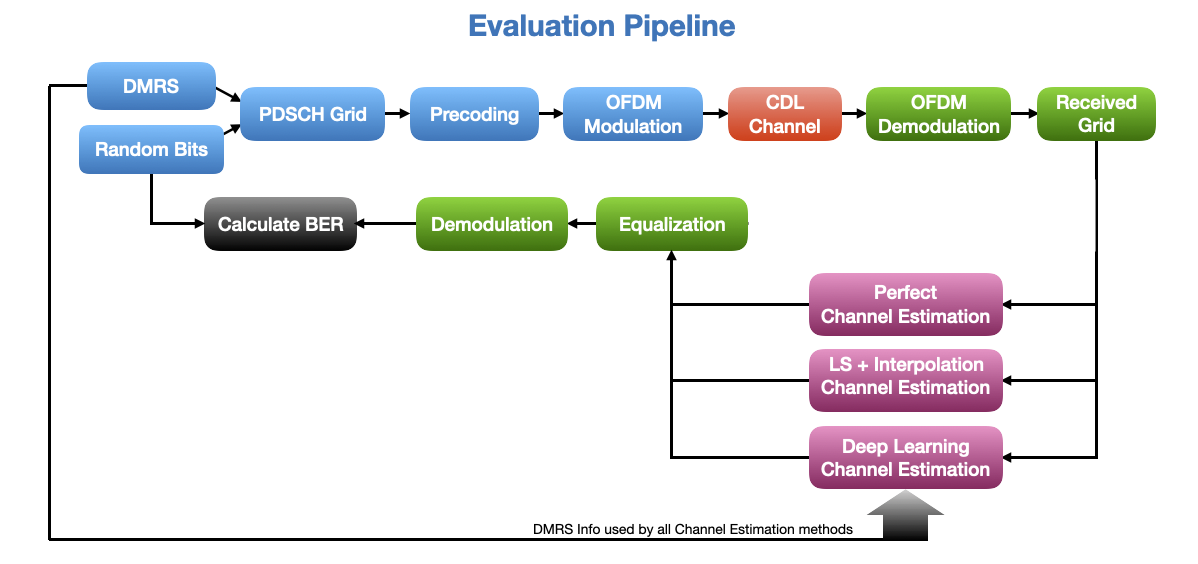
The following diagram shows the pipeline used for evaluation of our deep-learning-based channel estimator.
So, lets get started by importing the required modules.
[1]:
import numpy as np
import scipy.io
import time
import matplotlib.pyplot as plt
from neoradium import Carrier, PDSCH, CdlChannel, AntennaPanel, Grid, random
import torch
from torch import nn
Load the trained model
Here we define the channel estimator model and initialize it with the trained parameters.
[2]:
# ResNet Block
class ResBlock(nn.Module):
def __init__(self, inDepth, midDepth, outDepth, kernel=(3,3), stride=(1,1)):
super().__init__()
if isinstance(stride, int): stride = (stride, stride)
if isinstance(kernel, int): kernel = (kernel, kernel)
self.conv1 = nn.Conv2d(inDepth, midDepth, 1, stride, padding='valid') # 1x1 conv.
self.bn1 = nn.BatchNorm2d(midDepth)
self.conv2 = nn.Conv2d(midDepth, midDepth, kernel, padding='same')
self.bn2 = nn.BatchNorm2d(midDepth)
self.conv3 = nn.Conv2d(midDepth, outDepth, 1, stride, padding='valid') # 1x1 conv.
self.bn3 = nn.BatchNorm2d(outDepth)
self.relu = nn.ReLU(inplace=True)
self.downSampleNet = None
if ((stride != (1,1)) or (inDepth!=outDepth)):
self.downSampleNet = nn.Sequential(nn.Conv2d(inDepth, outDepth, 1, stride), # 1x1 conv.
nn.BatchNorm2d(outDepth) )
for bn in [self.bn1, self.bn2, self.bn3]:
nn.init.ones_(bn.weight)
nn.init.zeros_(bn.bias)
for conv in [self.conv1, self.conv2, self.conv3]:
nn.init.trunc_normal_(conv.weight, std=1/np.sqrt(np.prod(list(conv.weight.shape)[1:])))
nn.init.zeros_(conv.bias)
nn.init.zeros_(self.bn3.weight) # This could improve results. It makes the block start like identity.
def forward(self, x):
out = self.conv1(x)
out = self.bn1(out)
out = self.relu(out)
out = self.conv2(out)
out = self.bn2(out)
out = self.relu(out)
out = self.conv3(out)
out = self.bn3(out)
if self.downSampleNet is None: out += x
else: out += self.downSampleNet(x)
out = self.relu(out)
return out
# The Channel Estimator model
class ChEstNet(nn.Module):
def __init__(self):
super().__init__()
self.res1 = ResBlock(2, 16, 64, (9,11)) # Res Block 9x11 kernel
self.res2 = ResBlock(64, 16, 64, (3,7)) # Res Block 3x7 kernel
self.res3 = ResBlock(64, 16, 64, (3,7)) # Res Block 3x7 kernel
self.conv = nn.Conv2d(64, 2, 3, padding='same')
nn.init.trunc_normal_(self.conv.weight, std=1/np.sqrt(np.prod(list(self.conv.weight.shape)[1:])))
nn.init.zeros_(self.conv.bias)
def forward(self, x):
out = self.res1(x)
out = self.res2(out)
out = self.res3(out)
out = self.conv(out)
return out
# Checking GPU availability
device = "cuda" if torch.cuda.is_available() else "mps" if torch.backends.mps.is_available() else "cpu"
print("Using '%s' device."%({'cuda':'Cuda', 'mps':'Metal','cpu':'CPU'}[device]))
# Instantiate the model and move it to the target device
model = ChEstNet().to(device)
# Load the trained model parameters:
# Note: The model file "ChEstModel-300.pth" was trained with 300 epochs using a parameter search. It performs
# better than the model trained in the previous step with 100 epochs. You can try both by choosing the
# corresponding line below.
model.load_state_dict(torch.load('Models/ChEstModelWeights.pth', map_location=device)); # From prev. step.
# model.load_state_dict(torch.load('Models/ChEstModel-300.pth', map_location=device)); # Trained for 300 Epochs
model.eval(); # Set the model to evaluation mode
Using 'Cuda' device.
mlChanEst function
The mlChanEst function in the following cell receives the DMRS information, the received resource grid, and the trained model as input. It first calculates the channel estimates at the pilot locations using LS method and then converts these estimates to a set of L x K complex matrixes that are fed to the model for inference. (L is the number of OFDM symbols per slot and K is the number of subcarriers)
The model outputs another set of L x K matrixes which contain the predicted channel information. These matrixes are then re-packaged as a 4-D complex numpy array that is returned as the estimated channel.
[3]:
def mlChanEst(dmrs, rxGrid, model):
rsGrid = rxGrid.bwp.createGrid( len(dmrs.pxxch.portSet) ) # Create an empty resource grid
dmrs.populateGrid(rsGrid) # Populate the grid with DMRS values
rsIndexes = rsGrid.getReIndexes("DMRS") # This contains the locations of DMRS values
rr, ll, kk = rxGrid.shape # Number of RX antenna, Number of symbols, Number of subcarriers
pp, ll2, kk2 = rsGrid.shape # Number of Ports (From DMRS)
if (ll!=ll2) or (kk!=kk2): raise ValueError("The Gird size (%dx%d) does not match the DMRs (%dx%d)."%(ll,kk,ll2,kk2))
modelIn = []
for p in range(pp): # For each DMRS port (i.e. each layer)
portLs = rsIndexes[1][(rsIndexes[0]==p)] # Indexes of symbols containing pilots in this port
portKs = rsIndexes[2][(rsIndexes[0]==p)] # Indexes of subcarriers containing pilots in this port
ls = np.unique(portLs) # Unique Indexes of symbols containing pilots in this port
ks = portKs[portLs==ls[0]] # Unique Indexes of subcarriers containing pilots in this port
numLs, numKs = len(ls), len(ks) # Number of OFDM symbols and number of subcarriers
pilotValues = rsGrid[p,ls,:][:,ks] # Pilot values in this port
rxValues = rxGrid.grid[:,ls,:][:,:,ks] # Received values for pilot signals
hEst = np.transpose(rxValues/pilotValues[None,:,:], (1,2,0)) # Channel estimates at pilot locations (L,K,Nr)
for r in range(rr): # For each receiver antenna
inH = np.zeros((2,)+rxGrid.shape[1:], dtype=np.float64) # Create one 3D matrix with all zeros
for li,l in enumerate(ls):
inH[0,l,ks] = hEst[li,:,r].real # Set the LS estimates at pilot location (Real)
inH[1,l,ks] = hEst[li,:,r].imag # Set the LS estimates at pilot location (Imaginary)
modelIn += [ inH ]
# Package all inputs as a batch in a PyTorch tensor
modelIn = torch.from_numpy( np.float32(np.stack(modelIn)) ).to(device)
with torch.no_grad(): modelOut = model(modelIn) # Run inference for the whole batch
modelOut = modelOut.cpu().numpy() # Bring the results back to CPU and convert to numpy
estChan = np.transpose( modelOut.reshape((pp,rr)+modelOut.shape[1:]), (3,4,1,0,2) ) # Convert to a 5-D tensor
estChan = estChan[...,0] + 1j*estChan[...,1] # Convert to a 4-D complex tensor
return estChan
Evaluation Pipeline
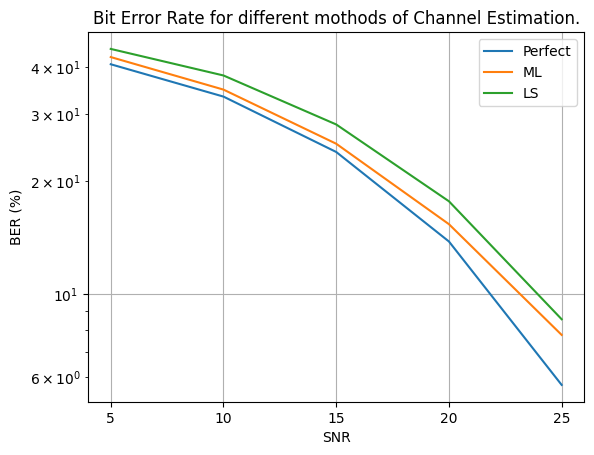
The following cell implements the evaluation pipeline as shown above. It runs the pipeline 3 times with perfect, ML, and LS channel estimation methods and prints the results at the end. As it can be seen, the ML-based channel estimation performs better than LS method which is based on interpolation.
[4]:
numFrames = 2 # Number of time-domain frames
snrDbs = [5,10,15,20,25] # SNR values (in dB) for which we want to evaluate the model
freqDomain = False # Set to True to apply channel in frequency domain
carrier = Carrier(numRbs=51, spacing=30) # Create a carrier with 51 RBs and 30KHz subcarrier spacing
bwp = carrier.curBwp # The only bandwidth part in the carrier
# Create a PDSCH object
pdsch = PDSCH(bwp, interleavingBundleSize=0, numLayers=2, nID=carrier.cellId, modulation="16QAM")
pdsch.setDMRS(prgSize=0, configType=2, additionalPos=2) # Specify the DMRS configuration
numSlots = bwp.slotsPerFrame*numFrames # Total number of slots
results = {} # Dictionary to save the results
for chanEstMethod in ["Perfect", "ML", "LS"]: # Three different channel estimation methods
results[chanEstMethod] = {}
print("\nSimulating end-to-end for \"%s\", with \"%s\" channel estimation, in %s domain."%
("16QAM", chanEstMethod, "frequency" if freqDomain else "time"))
print("SNR(dB) Total Bits Bit Errors BER(%) time(Sec.)")
print("------- ---------- ---------- ------ ----------")
for snrDb in snrDbs: # For each SNR value in snrDbs
random.setSeed(123) # Making the results reproducible for each SNR
t0 = time.time() # Start time for each SNR
carrier.slotNo = 0
# Creating a CdlChannel object
channel = CdlChannel('C', delaySpread=300, carrierFreq=4e9, dopplerShift=5,
txAntenna = AntennaPanel([2,2], polarization="x"), # 8 TX antenna
rxAntenna = AntennaPanel([1,1], polarization="+"), # 2 RX antenna
seed = 123,
timing = "nearest")
bitErrors = 0
totalBits = 0
for slotNo in range(numSlots):
grid = pdsch.getGrid() # Create a resource grid populated with DMRS
numBits = pdsch.getBitSizes(grid)[0] # Number of bits available in the resource grid
txBits = random.bits(numBits) # Create random binary data
pdsch.populateGrid(grid, txBits) # Map/modulate the data to the resource grid
# Store the indexes of the PDSCH data in pdschIndexes to be used later.
pdschIndexes = pdsch.getReIndexes(grid, "PDSCH")
# Getting the Precoding Matrix, and precoding the resource grid
channelMatrix = channel.getChannelMatrix(bwp) # Get the channel matrix
precoder = pdsch.getPrecodingMatrix(channelMatrix) # Get the precoder matrix from PDSCH object
precodedGrid = grid.precode(precoder) # Perform the precoding
if freqDomain:
rxGrid = precodedGrid.applyChannel(channelMatrix) # Apply the channel in frequency domain
rxGrid = rxGrid.addNoise(snrDb=snrDb) # Add noise
else:
txWaveform = precodedGrid.ofdmModulate() # OFDM Modulation
maxDelay = channel.getMaxDelay() # Get the max. channel delay
txWaveform = txWaveform.pad(maxDelay) # Pad with zeros
rxWaveform = channel.applyToSignal(txWaveform) # Apply channel in time domain
noisyRxWaveform = rxWaveform.addNoise(snrDb=snrDb, nFFT=bwp.nFFT) # Add noise
offset = channel.getTimingOffset() # Get timing info for synchronization
syncedWaveform = noisyRxWaveform.sync(offset) # Synchronization
rxGrid = syncedWaveform.ofdmDemodulate(bwp) # OFDM demodulation
if chanEstMethod == "Perfect": # Perfect Channel Estimation
estChannelMatrix = channelMatrix @ precoder[None,...]
elif chanEstMethod == "LS": # LS + Interpolation Channel Estimation
estChannelMatrix, noiseEst = rxGrid.estimateChannelLS(pdsch.dmrs, polarInt=False,
kernel='linear')
elif chanEstMethod == "ML": # ML-Based Channel Estimation
estChannelMatrix = mlChanEst(pdsch.dmrs, rxGrid, model)
else: assert(0)
eqGrid, llrScales = rxGrid.equalize(estChannelMatrix) # Equalization
rxBits = pdsch.getHardBitsFromGrid(eqGrid, pdschIndexes)[0] # Demodulation
bitErrors += np.abs(rxBits-txBits).sum() # Calculating number of bit errors
totalBits += numBits
print("\r %3d %8d %8d %6.2f %6.2f"%(snrDb, totalBits, bitErrors,
bitErrors*100/totalBits,time.time()-t0),end='')
carrier.goNext() # Prepare the carrier object for the next slot
channel.goNext() # Prepare the channel model for the next slot
dt = time.time()-t0 # Total time for this SNR
results[chanEstMethod][snrDb] = {"totalBits":totalBits,
"bitErrors":bitErrors,
"BER": bitErrors*100/totalBits,
"Time": dt}
print("\r %3d %8d %8d %6.2f %6.2f"%(snrDb, totalBits, bitErrors,
bitErrors*100/totalBits, dt))
# Compare the results in a plot:
for i,chanEstMethod in enumerate(['Perfect', 'ML', 'LS']):
bers = [results[chanEstMethod][snrDb]["BER"] for snrDb in snrDbs]
plt.plot(snrDbs, bers, label=chanEstMethod)
plt.legend()
plt.title("Bit Error Rate for different mothods of Channel Estimation.");
plt.grid()
plt.xlabel("SNR")
plt.xticks(snrDbs)
plt.ylabel("BER (%)")
plt.yscale('log')
plt.show()
Simulating end-to-end for "16QAM", with "Perfect" channel estimation, in time domain.
SNR(dB) Total Bits Bit Errors BER(%) time(Sec.)
------- ---------- ---------- ------ ----------
5 2545920 1036799 40.72 10.68
10 2545920 850716 33.41 10.37
15 2545920 606267 23.81 10.36
20 2545920 350625 13.77 10.40
25 2545920 145817 5.73 10.51
Simulating end-to-end for "16QAM", with "ML" channel estimation, in time domain.
SNR(dB) Total Bits Bit Errors BER(%) time(Sec.)
------- ---------- ---------- ------ ----------
5 2545920 1082460 42.52 10.93
10 2545920 887201 34.85 10.81
15 2545920 636788 25.01 10.74
20 2545920 388967 15.28 10.62
25 2545920 196876 7.73 10.67
Simulating end-to-end for "16QAM", with "LS" channel estimation, in time domain.
SNR(dB) Total Bits Bit Errors BER(%) time(Sec.)
------- ---------- ---------- ------ ----------
5 2545920 1138786 44.73 10.64
10 2545920 968019 38.02 10.74
15 2545920 717426 28.18 10.73
20 2545920 448406 17.61 10.74
25 2545920 217902 8.56 10.71
[ ]: