Channel timing

This notebooks shows the timing characteristics of a CDL channel model as it is applied to input signals for a duration of 100 slots.

import numpy as np
import scipy.io
import time
import matplotlib.pyplot as plt

from neoradium import Carrier, Modem, CdlChannel, AntennaPanel, Grid, Waveform, random
from neoradium.utils import getNmse, getMse

# Create a random grid and the corresponding TX waveform
carrierFreq=4e9 # 4 GHz

carrier = Carrier(startRb=0, numRbs=25, spacing=30) # Also try other subcarrier spacing values
bwp = carrier.curBwp
txGrid = bwp.createGrid(numPlanes=8)

stats = txGrid.getStats()
modem = Modem("16QAM")
numRandomBits = stats['UNASSIGNED']*modem.qm

bits = random.bits(numRandomBits)
symbols = modem.modulate(bits)

indexes = txGrid.getReIndexes("UNASSIGNED")
txGrid[indexes] = symbols

txWaveform = txGrid.ofdmModulate(carrierFreq)
print(bwp)
print("Shape of transmitted signal in time domain:",txWaveform.shape)

Bandwidth Part Properties:
  Resource Blocks:    25 RBs starting at 0 (300 subcarriers)
  Subcarrier Spacing: 30 KHz
  CP Type:            normal
  bandwidth:          9 MHz
  symbolsPerSlot:     14
  slotsPerSubFrame:   2
  nFFT:               1024
  frameNo:            0
  slotNo:             0

Shape of transmitted signal in time domain: (8, 15360)

# No Channel and no noise performance: ofdmModulate -> ofdmDemodulate
rxGridTD = txWaveform.ofdmDemodulate(bwp, f0=carrierFreq)
print(f"NMSE: {getNmse(txGrid.grid,rxGridTD.grid)}")
print(f"MAE: {np.abs(txGrid.grid-rxGridTD.grid).max()}")

NMSE: 4.011172718876436e-32
MAE: 8.005932084973443e-16

# Create a CDL-D channel
channel = CdlChannel(bwp, 'D', delaySpread=300, carrierFreq=4e9, dopplerShift=15,
                     txAntenna = AntennaPanel([2,4], polarization="|"),  # 8 TX antenna
                     rxAntenna = AntennaPanel([1,2], polarization="|"),  # 2 RX antenna
                     seed = 1234)
channel

CDL-D Channel Properties:
  carrierFreq:          4 GHz
  normalizeGains:       True
  normalizeOutput:      True
  txDir:                Downlink
  filterLen:            16 samples
  delayQuantSize:       64
  stopBandAtten:        80 db
  dopplerShift:         15 Hz
  coherenceTime:        0.028209479177387815 Sec.
  delaySpread:          300 ns
  ueDirAZ:              0.0°, 90.0°
  Cross Pol. Power:     11 db
  angleSpreads:         5° 8° 3° 3°
  TX Antenna:
    Total Elements:     8
    spacing:            0.5𝜆, 0.5𝜆
    shape:              2 rows x 4 columns
    polarization:       |
    Orientation (𝛼,𝛃,𝛄): 0° 0° 0°
  RX Antenna:
    Total Elements:     2
    spacing:            0.5𝜆, 0.5𝜆
    shape:              1 rows x 2 columns
    polarization:       |
    Orientation (𝛼,𝛃,𝛄): 0° 0° 0°
  hasLOS:               True
  LOS Path:
    Delay (ns):         0.00000
    Power (db):         -0.20000
    AOD (Deg):          0
    AOA (Deg):          -3
    ZOD (Deg):          1
    ZOA (Deg):          1
  NLOS Paths (13):
    Delays (ns):        0.000 10.50 183.6 408.9 421.5 541.2 778.8 532.5 1212. 2381. 2827. 2912.
                        3757.
    Powers (db):        -13.5 -18.8 -21.0 -22.8 -17.9 -20.1 -21.9 -22.9 -27.8 -23.6 -24.8 -30.0
                        -27.7
    AODs (Deg):         0    89   89   89   13   13   13   35   -64  -33  53   -132
                        77
    AOAs (Deg):         -180 89   89   89   163  163  163  -137 74   128  -120 -9
                        -84
    ZODs (Deg):         98   86   86   86   98   98   98   98   88   91   104  80
                        86
    ZOAs (Deg):         82   87   87   87   79   79   79   78   74   78   87   71
                        73

# Apply the channel in time domain:
maxDelay = channel.getMaxDelay()
paddedTxWaveform = txWaveform.pad(maxDelay)              # Pad the waveform with zeros
rxWaveform = channel.applyToSignal(paddedTxWaveform)     # Apply the channel to the waveform

syncedWaveform = rxWaveform.sync(channel.chanOffset)                 # Synchronization
rxGridTd = syncedWaveform.ofdmDemodulate(bwp, f0=carrierFreq)

# Apply the channel in frequency domain and compare
chanMat = channel.getChannelMatrix()
rxGridFd = txGrid.applyChannel(chanMat)
print(f"NMSE: {getNmse(rxGridFd.grid,rxGridTd.grid)}")

NMSE: 7.131743705718165e-05

# Apply the channel to 100 slots of input signal
chanMats = []
for s in range(100):
    # Go to next slot and do it again:
    channel.goNext()

    txGrid = bwp.createGrid(numPlanes=8)

    stats = txGrid.getStats()
    numRandomBits = stats['UNASSIGNED']*modem.qm

    bits = random.bits(numRandomBits)
    symbols = modem.modulate(bits)

    indexes = txGrid.getReIndexes("UNASSIGNED")
    txGrid[indexes] = symbols

    txWaveform = txGrid.ofdmModulate(carrierFreq)

    # Apply the channel in time domain:
    maxDelay = channel.getMaxDelay()
    paddedTxWaveform = txWaveform.pad(maxDelay)              # Pad the waveform with zeros
    rxWaveform = channel.applyToSignal(paddedTxWaveform)     # Apply the channel to the waveform

    syncedWaveform = rxWaveform.sync(channel.chanOffset)                 # Synchronization
    rxGridTd = syncedWaveform.ofdmDemodulate(bwp, f0=carrierFreq)

    # Apply the channel in frequency domain and compare
    chanMat = channel.getChannelMatrix()
    rxGridFd = txGrid.applyChannel(chanMat)
    assert getNmse(rxGridFd.grid,rxGridTd.grid)<1e-3
    chanMats += [chanMat]

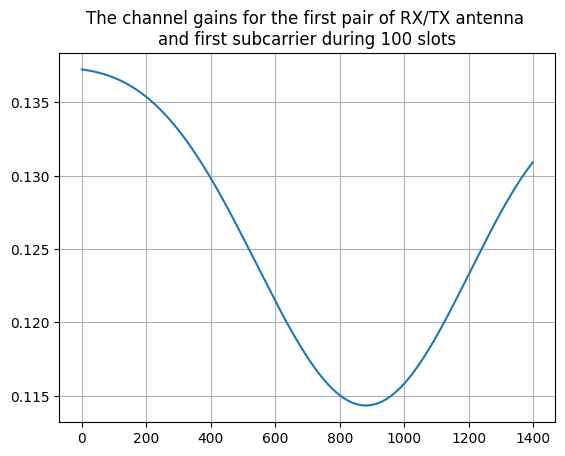
gs = np.concatenate([chanMat[:,0,0,0] for chanMat in chanMats])
plt.plot(np.abs(gs))
plt.title("The channel gains for the first pair of RX/TX antenna \n"+
          "and first subcarrier during 100 slots")
plt.grid()